BUAT LATIHAN TOPIK FUNGSI MATEMATIK TAMBAHAN DENGAN ANAK

Selepas PMR, Kak Tini masuk ke kelas sains tulen. Kak Tini sambung belajar di MRSM Jasin. Masa tu memang culture shock jugak sebab sebelum ni Kak Tini bersekolah di sekolah all-girls. Alih-alih, masuk MRSM, sekolah co-ed gais. Macam rusa masuk kampung lah citer dia. 2 tahun belajar di MRSM penuh dengan pelbagai kenangan manis yang tidak akan Kak Tini lupakan. 

Okay, sekarang ni bukan nak cerita pasal kenangan manis tapi nak cerita tentang mata pelajaran yang dipelajari. So, since Kak Tini amik jurusan sains tulen, secara automatik kena la ambik Matematik Tambahan kan. All along dengan 3 serangkai, Biologi, Kimia dan Fizik.

Masa tingkatan 4, dah la culture shock, belajar Add Maths guna buku warna ungu gelap yang sangat mencabar pulak tu, Ya Allah, rasa susah bebeno lahaiiii. Fast forward, gedebak-gedebuk, alhamdulillah, berjaya jugak dalam SPM. Masuk matriks, then terus degree. Tiba-tiba, jumpa balik si Add Maths ni. Hahahaha. Calculus I dan Calculus II pulak tu. Pengsan, bangun, pengsan, bangun la citer dia. Hehehehe. Alhamdulillah, berjaya jugak menggenggam segulung ijazah.

Dia camni. Dia macam alah bisa tegal biasa gitu. Kiranya, masa kat universiti, apa yang kita dah belajar zaman sekolah tu rasa kacang je. Masa tu, mulalah fikir, kenapalah masa Form 4, Form 5 dulu jenuh jugak la nak faham ek? Padahal, sekarang ni senang je nak buat. Haa, gitu.

Now, selalu jugak la dok buat latihan add maths sebab kengkadang dok sama-sama selesaikan soalan homework anak. Ala-ala buat study group gituh. Malulah kang tetiber ibunya tak tahu buat pulak kan? Kena always asah skill ooooo. Anyway, haritu ada buat latihan pasal fungsi, so, anak-anak sekalian, bolehlah check it out nota ringkas dan latihan fungsi kat bawah ni hokey. Selamat belajar!

PENGENALAN KEPADA FUNGSI

Dalam matematik, fungsi adalah satu hubungan istimewa antara nilai-nilai: setiap nilai input (x) berkaitan dengan tepat satu nilai output (y). Fungsi terdapat di mana-mana dalam matematik dan penting untuk memahami dunia di sekeliling kita, dari meramalkan cuaca hingga mengaturcara komputer.

Apakah Itu Fungsi?

Fungsi boleh dianggap sebagai mesin yang mengambil input, memprosesnya, dan menghasilkan output. Hubungan ini sering ditulis sebagai f(x), yang mana f mewakili fungsi dan x mewakili input. Output biasanya dirujuk sebagai y.

Sebagai contoh:

Diberikan fungsi f(x)=x+2. Cari nilai y apabila x=3

Langkah 1: Tulis fungsi yang diberikan.

f(3)=x+2

Langkah 2: Gantikan x=3 ke dalam fungsi.

y=3+2

Langkah 3: Selesaikan persamaan.

y=5

Jawapan: Nilai y ialah 5 apabila x=3

Jalan kerja:

f(x)=x+2. Cari nilai y apabila x=3

f(3)=x+2

y=3+2

y=5

Konsep fungsi ini penting untuk memahami bagaimana pelbagai pemboleh ubah dalam kehidupan sebenar berkaitan antara satu sama lain. Sebagai contoh, suhu di luar rumah boleh menjadi fungsi masa dalam sehari, atau jumlah wang yang korang miliki boleh menjadi fungsi bilangan jam korang bekerja.

Jenis-Jenis Fungsi

Fungsi Linear

Fungsi ini membentuk garis lurus apabila dilukis grafnya.
Bentuk umum adalah f(x)=mx+c, di mana m adalah kecerunan dan c adalah pintasan-y.

Jom kita tengok contoh fungsi linear: f(x)=2x+1

Langkah 1: Kenal pasti nilai m dan c.

m=2 (kecerunan)

c=1 (pintasan-y)

Langkah 2: Tulis semula fungsi dengan nilai m dan c yang telah dikenal pasti.

f(x)=2x+1

Langkah 3: Pilih nilai x untuk mencari nilai f(x) Sebagai contoh, jika x=3

f(3)=2(3)+1

Langkah 4: Selesaikan persamaan.

f(3)=6+1

f(3)=7

Jawapan:

Apabila x=3

Nilai f(x) ialah 7.

Jalan kerja:

f(x)=2x+1, jika x=3

f(3)=2(3)+1

f(3)=6+1

f(3)=7

Fungsi linear sering digunakan dalam kehidupan seharian untuk meramalkan dan memodelkan hubungan langsung antara dua pemboleh ubah. Sebagai contoh, jika korang mendapat gaji tetap per jam, jumlah pendapatan korang adalah fungsi linear masa yang korang bekerja.

 

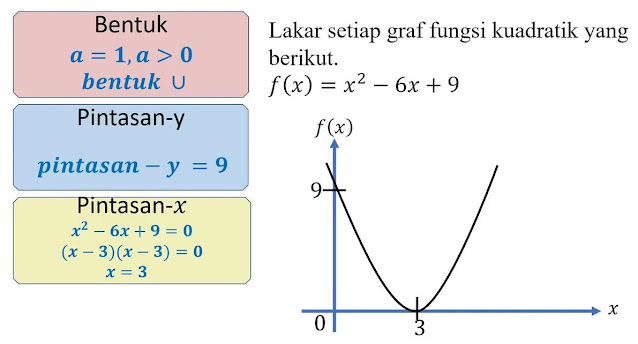
Fungsi Kuadratik

Fungsi ini membentuk parabola apabila dilukis grafnya.

Bentuk umum fungsi kuadratik adalah: f(x)=ax^2+bx+c yang mana a, b, dan c adalah pemalar (konstan) dan x adalah pemboleh ubah.

Jom kita tengok contoh fungsi kuadratik: f(x)=x^2−4x+3

Langkah 1: Kenal pasti nilai a, b, dan c.

a=1 (koefisien untuk x^2)

b=−4 (koefisien untuk x)

c=3 (pemalar)

Langkah 2:

Tulis semula fungsi dengan nilai a, b, dan c yang telah dikenal pasti

f(x)=x^2−4x+3

Langkah 3:

Pilih nilai x untuk mencari nilai f(x). Sebagai contoh, jika x=2.

f(2)=(2)^2−4(2)+3

Langkah 4: Selesaikan persamaan.

f(2)=4−8+3

f(2)=−1

Jawapan: 

Apabila x=2x = 2x=2, nilai f(x) ialah -1.

Jalan kerja:

f(x)=x^2−4x+3, jika x=2.

f(2)=(2)^2−4(2)+3

f(2)=4−8+3

f(2)=−1

Fungsi kuadratik sering muncul dalam masalah yang melibatkan objek yang dilemparkan ke udara. Trajektori objek tersebut, di bawah pengaruh graviti, akan membentuk parabola.

Contoh: Jika korang melemparkan bola ke udara, ketinggian bola adalah fungsi kuadratik masa.

Fungsi Kubik

Fungsi ini membentuk lengkung berbentuk S apabila dilukis grafnya.

Bentuk umum fungsi kubik adalah: f(x)=ax^3+bx^2+cx+d yang mana a, b, c, dan d adalah pemalar (konstan) dan x adalah pemboleh ubah.

Contoh:

Jom kita lihat contoh fungsi kubik: f(x)=x^3−3x^2+2x

Langkah 1: Kenal pasti nilai a, b, c, dan d.

a=1 (koefisien untuk x^3)

b=−3 (koefisien untuk x^2)

c=2 (koefisien untuk x)

d=0 (tiada pemalar tetap dalam contoh ini)

Langkah 2: Tulis semula fungsi dengan nilai a, b, c, dan d yang telah dikenal pasti.

f(x)=x^3−3x^2+2x

Langkah 3: Pilih nilai x untuk mencari nilai f(x). Sebagai contoh, jika x=1.

f(1)=(1)^3−3(1)^2+2(1)

Langkah 4: Selesaikan persamaan.

f(1)=1−3+2

f(1)=0

Jawapan: 

Apabila x=1, nilai f(x) ialah 0.

Jalan kerja:

f(x)=x^3−3x^2+2x, jika x=1.

f(1)=(1)^3−3(1)^2+2(1)

f(1)=1−3+2

f(1)=0

Fungsi kubik digunakan dalam pelbagai aplikasi sains dan kejuruteraan untuk memodelkan hubungan yang lebih kompleks yang tidak dapat diterangkan oleh fungsi linear atau kuadratik.

Contoh: Dalam kejuruteraan, fungsi kubik boleh digunakan untuk memodelkan kelajuan enjin kereta pada pelbagai tahap penggunaan bahan api.

Fungsi Eksponen

Fungsi ini mempunyai bentuk f(x)=ax, di mana a adalah satu pemalar.

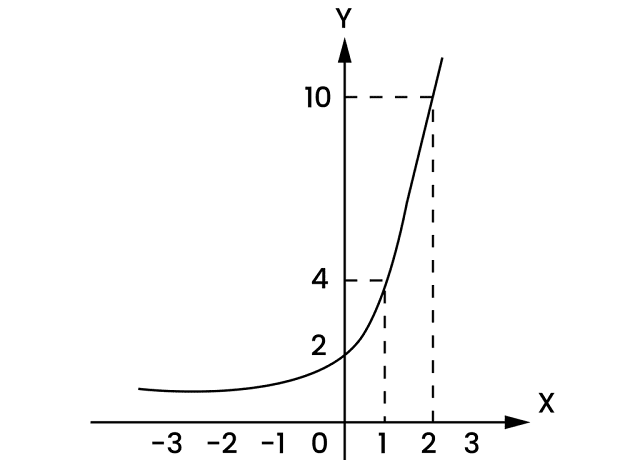
Contoh: f(x)=2x.

Fungsi eksponen sangat penting dalam memahami fenomena pertumbuhan seperti pertumbuhan populasi, pertumbuhan bakteria, dan juga dalam bidang kewangan untuk memahami faedah kompaun.

Contoh: Pertumbuhan wang dalam akaun simpanan dengan faedah kompaun adalah fungsi eksponen masa.

 

Konsep Utama

Domain dan Julat

Domain sesuatu fungsi adalah set semua nilai input yang mungkin (nilai-nilai x).
Julat sesuatu fungsi adalah set semua nilai output yang mungkin (nilai-nilai y).

Memahami domain dan julat membantu kita menggunakan fungsi dengan betul dan mengelakkan kesilapan dalam pengiraan atau interpretasi data.

Contoh:

Fungsi 𝑓(𝑥)=𝑥^2

Domain: Semua nombor nyata (tiada sekatan)

Julat: 𝑦≥0 kerana mengkuadratkan nombor sentiasa menghasilkan nilai yang tidak negatif.

Fungsi: 𝑓(𝑥)=𝑥  

Domain: 𝑥≥0 kerana kita tidak boleh mengambil punca kuasa dua dari nombor negatif

Julat: 𝑦≥0 kerana punca kuasa dua nombor tidak pernah negatif.

Sumber: Klik kat sini

Fungsi Gubahan

Ini adalah fungsi yang dibentuk dengan menggabungkan dua fungsi.
Jika f(x)f(x)f(x) dan g(x)g(x)g(x) adalah dua fungsi, maka fungsi gubahan (f∘g)(x)(f \circ g)(x)(f∘g)(x) didefinisikan sebagai f(g(x))f(g(x))f(g(x)).

Contoh: Jika f(x)=x+2f(x) = x + 2f(x)=x+2 dan g(x)=x2g(x) = x^2g(x)=x2, maka (f∘g)(x)=f(g(x))=f(x2)=x2+2(f \circ g)(x) = f(g(x)) = f(x^2) = x^2 + 2(f∘g)(x)=f(g(x))=f(x2)=x2+2.

Fungsi gubahan membolehkan kita memodelkan situasi di mana satu proses bergantung kepada hasil proses lain, memberikan kita alat yang kuat untuk analisis dan penyelesaian masalah.

Contoh: Jika f(x)f(x)f(x) mewakili keuntungan bulanan dan g(x)g(x)g(x) mewakili jumlah jualan bulanan, (f∘g)(x)(f \circ g)(x)(f∘g)(x) boleh memberi kita gambaran tentang bagaimana perubahan dalam jualan mempengaruhi keuntungan.

Sumber: Klik kat sini

Fungsi Songsang

Fungsi songsang membalikkan operasi fungsi asal.
Jika f(x)f(x)f(x) adalah satu fungsi, fungsi songsangnya dilambangkan sebagai f−1(x)f^{-1}(x)f−1(x).
Untuk fungsi f(x)=2x+3f(x) = 2x + 3f(x)=2x+3, fungsi songsang adalah f−1(x)=x−32f^{-1}(x) = \frac{x - 3}{2}f−1(x)=2x−3.
Fungsi songsang penting dalam banyak bidang termasuk penyulitan data, di mana kita perlu membalikkan proses untuk mendapatkan kembali maklumat asal.

Contoh: Jika fungsi f(x)f(x)f(x) mewakili pengiraan harga selepas dikenakan cukai, fungsi songsangnya f−1(x)f^{-1}(x)f−1(x) boleh digunakan untuk mencari harga asal sebelum dikenakan cukai.

Aplikasi Fungsi dalam Kehidupan Seharian

Fungsi bukan sahaja konsep teori; ia mempunyai aplikasi praktikal dalam banyak bidang. Sebagai contoh:

1) Ekonomi: Fungsi digunakan untuk memodelkan hubungan antara pelbagai pemboleh ubah ekonomi, seperti penawaran dan permintaan. Harga barang boleh menjadi fungsi jumlah barang yang ditawarkan dan jumlah barang yang diminta.

2) Biologi: Pertumbuhan populasi boleh dimodelkan menggunakan fungsi eksponen. Pertumbuhan bakteria dalam makmal sering mengikuti corak eksponen pada fasa awal pertumbuhan.

3) Kejuruteraan: Fungsi menerangkan fenomena fizikal seperti trajektori projektil atau aliran elektrik. Jurutera menggunakan fungsi untuk meramalkan bagaimana objek akan bertindak balas dalam situasi tertentu.

Soalan Latihan

1) Kenal pasti jenis fungsi:

a) f(x)=3x+4f(x) = 3x + 4f(x)=3x+4

b) g(x)=x2−5x+6g(x) = x^2 - 5x + 6g(x)=x2−5x+6

2) Cari fungsi gubahan:

a) f(x)=2xf(x) = 2xf(x)=2x
b) g(x)=x+1g(x) = x + 1g(x)=x+1

3) Tentukan fungsi songsang:

a) f(x)=3x−24f(x) = \frac{3x - 2}{4}f(x)=43x−2

4) Cari domain dan julat fungsi:

a) f(x)=x−1f(x) = \sqrt{x - 1}f(x)=x−1
b) g(x)=1xg(x) = \frac{1}{x}g(x)=x1

5) Gambarkan graf fungsi:

a) f(x)=−x2+4x−3f(x) = -x^2 + 4x - 3f(x)=−x2+4x−3
b) g(x)=x3−2x2+x−1g(x) = x^3 - 2x^2 + x - 1g(x)=x3−2x2+x−1

Memahami fungsi adalah penting untuk menguasai matematik. Dengan memahami cara mengenal pasti, memanipulasi, dan menerapkan pelbagai jenis fungsi, korang akan dilengkapi dengan baik untuk menangani pelbagai masalah, baik dalam peperiksaan SPM mahupun dalam kehidupan sebenar.  Selamat belajar!

Thanks for reading everyone. Jumpa lagi di entri yang lain.

FROM THE RIVER TO THE SEA, PALESTINE WILL BE FREE

xoxo